紧固件作为通用基础件,是工程和制造中不可或缺的重要组成部分。在航空航天领域,飞机连接依赖各类紧固件,可确保飞行器的结构牢固可靠,飞行器部段之间的连接也离不开紧固件的支持。因此,螺栓连接的可靠性对于保障航空航天飞行器的安全和稳定运行至关重要[1]。
当前常用的机械连接方式中,螺栓连接是一种可拆卸的固定连接,具有结构简单、连接可靠、装拆方便等优点。SUN和LIAO等[2-3]通过对螺纹的建模和分析,得到螺纹轴向载荷和应力分布规律,研究了螺纹的形状和螺栓效应对螺栓疲劳的影响,研究结果对建立螺栓疲劳模型提供了理论上的帮助,利用有限元仿真分析等技术,对螺栓连接在循环载荷下的疲劳性能进行模拟和预测。PAI等[4]通过建立复杂的有限元模型,结合材料的自身结构、载荷历程和几何非线性等因素,实现了对螺栓连接疲劳寿命的准确预测。HOUSARI等[5]开展了针对螺栓连接应力松弛现象的仿真研究,通过分析材料的弹性和塑性行为,模拟了预紧后螺栓连接的应力状态变化,研究结果为应力松弛影响的评估提供了理论基础。MAGGI等[6]对螺栓进行仿真分析,研究了疲劳载荷和应力松弛对螺栓连接寿命的综合影响。ZHANG等[7]开发了一种多尺度仿真方法,用于研究复杂工况下的螺栓连接疲劳行为。吕金峄等[8]发现某摇臂螺栓在使用过程中因偏载而发生疲劳断裂,并研究了外载荷对螺栓连接疲劳行为的影响。
综上所述,国内外学者已针对螺纹副的仿真建模进行了大量研究,但是对于螺纹副服役搭接疲劳可靠性的仿真方法及预测模型研究还不充分,还不能形成相应的仿真数据库。基于以上研究现状,笔者以典型材料螺纹副为研究对象,构建了仿真模型,获取螺栓连接的有限元关键建模方法,为后续的螺栓服役及正向设计提供分析方法,同时建立了典型工况下螺纹副服役搭接疲劳的仿真模型,并对影响服役的关键因素进行分析,结果可为后续典型螺纹副服役及可靠性提供数据支撑。
1. 螺纹连接疲劳仿真分析模型
基于GJB 715.9—1990 《紧固件试验方法 抗剪接头疲劳》,建立了典型材料螺纹连接的疲劳仿真分析模型,研究螺栓连接在疲劳载荷下的应力应变分布、裂纹生成与扩展规律,并评估了不同因素对搭接疲劳寿命的影响。通过有限元仿真和试验验证相结合的方法,确定了影响螺栓连接性能的关键因素,为设计优化和可靠性评估提供理论依据。
1.1 螺栓搭接疲劳有限元建模方法
利用ABAQUS软件建立了单螺栓搭接结构的有限元模型,包含螺栓、螺母、被连接板及垫片等部件。采用的螺栓为M6标准件,符合GB/T 5782—2016 《六角头螺栓》要求,螺母同样为M6标准件,符合GB/T 41—2000 《六角螺母 C级》要求,圆垫片的外径为11 mm,内径为6.6 mm,厚度为1.5 mm,被连接板的尺寸为96 mm×48 mm×6 mm(长度×宽度×高度)。
在建立有限元模型时,首先采用CAD软件绘制螺栓、螺母及垫片的几何模型,然后在ABAQUS软件中进行网格划分,模型采用的网格单元类型为C3D8R线性缩减积分单元,并对螺纹处的网格进行局部细化处理,以更准确地模拟应力集中效应。该方法得到的螺纹部分单元形状规则,螺纹处网格细节如图1所示。
1.2 边界条件及载荷设置
有限元模型的边界条件及载荷设置至关重要,有利于确保仿真结果的准确性和可靠性。单螺栓搭接结构有限元模型如图2所示。首先,对固定板的左端面施加运动耦合约束,将其与参考点1连接,对参考点1施加完全约束。将螺母整体与参考点3进行运动耦合约束,并对参考点3施加绕z轴的转角位移,通过螺纹间的相对运动实现螺栓的拉紧,进而施加预紧力。
为模拟实际工作环境中的疲劳载荷情况,将移动板的右端面与参考点2进行运动耦合约束,对参考点2施加应力比为0.1的正弦位移载荷,其中载荷峰值为Pm,载荷频率为ω。此过程模拟了螺栓连接在循环载荷作用下的疲劳行为。通过对参考点2施加周期性位移载荷,观察螺栓连接的应力应变分布及裂纹扩展规律。
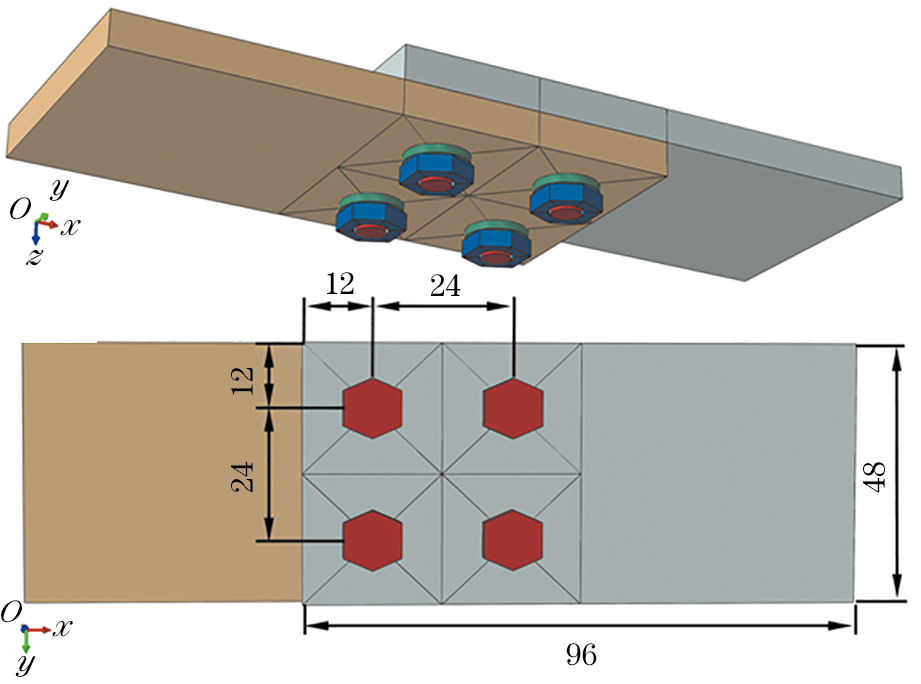
根据标准GJB 715.9—1990,在单螺栓搭接结构有限元模型的基础上,进一步建立多螺栓搭接结构有限元模型,结果如图3所示。多螺栓搭接结构的螺栓、螺母及垫片尺寸保持不变,被连接件及搭接相关尺寸按照标准GJB 715.9—1990的规定进行设置。材料参数、边界条件及外部载荷等方面的设置均与单螺栓搭接结构有限元模型保持一致,以确保两种模型的对比分析具有一致性和可比性。
1.3 材料参数设定
螺栓和螺母均采用TC4合金材料,建立了其典型金属弹性和塑性本构模型。材料参数通过准静态拉伸试验获取,弹性模量为93.2 GPa,泊松比为0.34,塑性参数如表1所示[9]。被连接件材料为TC4和Al6061合金,分别建立其金属弹性和塑性本构模型。TC4合金的弹性模量为80 GPa,泊松比为0.34;Al6061合金的弹性模量为70 GPa,泊松比为0.27。采用Johnson-Cook本构模型,本构方程如式(1)所示,具体参数如表2所示。
| �¯=[�+�(�¯)�][1+�ln(�˙�˙0)][1-(�-�room�melt-�room)�] | (1) |
式中:A为准静态屈服强度;B为硬化模量;C为应变率敏感系数;n为硬化指数;�¯为塑性应变;�˙为应变率;�˙0为参考应变率;m为温度软化指数;T为材料的绝对温度;Troom为参考温度;Tmelt为材料的熔点温度;�¯为应力。
| 塑性应力/MPa | 塑性应变 | 塑性应力/MPa | 塑性应变 |
|---|---|---|---|
| 1 058.21 | 0 | 1 295.17 | 0.066 58 |
| 1 119.05 | 0.002 28 | 1 302.38 | 0.071 61 |
| 1 145.73 | 0.004 83 | 1 308.46 | 0.076 65 |
| 1 168.36 | 0.007 53 | 1 315.10 | 0.081 70 |
| 1 210.18 | 0.008 98 | 1 322.22 | 0.086 69 |
| 1 237.48 | 0.016 97 | 1 328.67 | 0.091 53 |
| 1 259.50 | 0.028 28 | 1 335.59 | 0.096 42 |
| 1 277.74 | 0.046 03 | 1 342.71 | 0.101 35 |
| 1 282.10 | 0.057 05 | 1 348.41 | 0.106 28 |
| 1 288.43 | 0.061 54 | 1 354.86 | 0.111 04 |