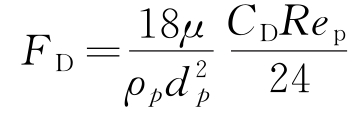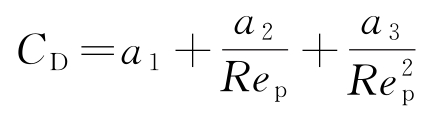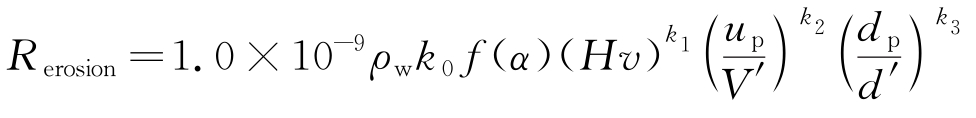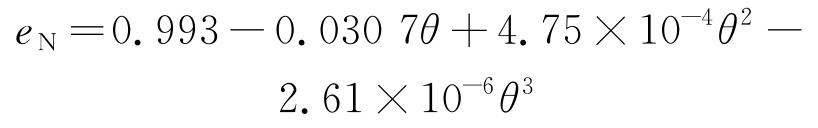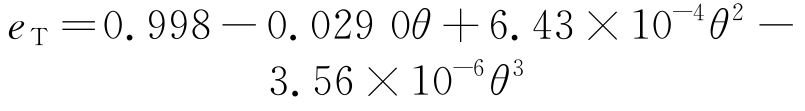管道内多相流的冲蚀研究始终是一个焦点，大量的实践证明通过计算流体力学（CFD）方法对管道的冲蚀磨损行为进行数值模拟具有极可靠的计算精度的。ZHAO等[1]结合了计算流体动力学（CFD）和离散元方法（DEM），模拟了液固流动特性对90°弯管的冲蚀影响，结果证明随着颗粒体积分数的增加、弯管表面冲蚀程度增加。LIU等[2]将两相流模型与多颗粒冲击水平管壁表面的冲蚀预测模型相结合，获得了预测水平壁侵蚀的简化方法，并得出管壁均匀减薄的主要原因是颗粒在很小的冲击角度下不断冲击壁面。ZHANG等[3]通过流体速度、颗粒直径和质量流量分析了三通管道冲蚀速率与壁面剪切应力之间的关系。ZHU等[4]基于欧拉-拉格朗日方法和冲计算流体动力学离散相位模型（CFD-DPM）求解了液固流并预测了冲蚀分布，结果表明冲蚀主要发生在U型弯管的下表面和下游管的外表面。

目前对于管道冲蚀磨损的研究已经不再停留于输送工况和影响参数等，对于管道本身结构对冲蚀磨损的影响得到了国际上众多学者的密切关注。ZHOU等[5]设计了具有双层壁结构的弯头，以呈现冲蚀特性、颗粒破损率和压降，研究了弯管形状对冲蚀的影响规律。陈铮等[6]在异径偏心弯管冲蚀模拟中发现，变径后的直管段剪切应力较大，易发生冲蚀。OTHAYQ等[7]通过试验和计算研究了两个弯头之间距离对第二弯头上固体颗粒冲蚀行为的影响，发现距离越长，粒子在撞击第一个弯头后恢复和增加其动能之前的时间就越多，在第二个弯头上就有更大的冲蚀风险。ZHAO等[8]研究表明串联弯管下游弯头的冲蚀情况受连接距离的影响较大，且当颗粒粒径很大时，最初弯头处冲蚀程度很大，在后续串联弯头处的冲蚀程度反而相对较小。王森等[9]分析发现π形管连接长管条件下，第4个弯头受冲蚀程度最大。SEDREZ等[10]验证了串联弯管方向的改变也会影响弯头处的冲蚀程度。

在实际工程应用中，CO2驱油是一种高效、无污染的油气开采技术，该技术使用条件广泛且成本低，大量实践证明CO2是一种有效的驱油剂，可有效降低原油黏度和油水间的界面张力。SUN等[11]通过实验验证了CO2-水-原油混合流体的有效黏度是随CO2溶液压力的增加呈指数下降的；但随着黏度的降低，砂粒受到的黏性力束缚作用减弱，冲蚀速率提高。MA等[12]研究发现，黏度是影响冲蚀的重要物理化学特性，流体黏度越高，形成的冲蚀风险越低。LUO等[13]也验证了高黏度液体会延迟颗粒对壁面的射流冲击，降低冲击强度、减少冲蚀。同时CO2在注入油层发生混相效应的过程中，也会与混合的水相发生反应，生成的碳酸对管壁具有较强的腐蚀性，也会增加壁面冲蚀速率。综上，笔者对流动条件下含CO2原油对管壁的冲蚀影响因素进行研究，并对管道结构进行优化调整，以期有效减小管壁冲蚀程度，提高管道寿命。

1. 计算模型

1.1 流体控制方程

数值模拟用连续相介质的液相为80%（体积分数，下同）的油和20%的水，气相为CO2，离散相的固相为砂粒。由于油和水在流动过程中，并非混合在一起，选用欧拉非均质模型。选用适合描述管道内二次流迪恩涡的Realizable k-ε湍流模型作为黏性模型进行湍流模拟，近壁面处理采用标准壁面函数。本研究中不涉及温度对模拟结果的影响，因此只采用Naiver-Stokes方程组中的质量守恒和动量守恒方程：

固相砂粒是微小颗粒，采用DPM模型可以较准确地描述运动状态，与连续相能做到双向耦合。离散相颗粒受力控制方程可以用来描述其运动轨迹，具体为：

式中：ρ为连续相密度（kg/m3）；t为时间（s）；u为连续相速度（m/s）；P为压力（Pa）；τ为作用在流体微元的黏性应力（N）；ρg为连续相重力（N）；SM为离散相对连续相产生的动量增量（kg·m/s）；up为离散相颗粒速度（m/s）；μ为连续相动力黏度（Pa·s）；ρp为离散相颗粒密度（kg/m3）；gx为沿着x方向的重力加速度分量（m/s2）；Fx为沿着x方向上的其他作用力（N）；dp为颗粒直径（m）；Re为雷诺系数；CD为拖拽力系数。

1.2 冲蚀模型

目前，多种冲蚀模型已在国际上被提出。PARSI等[14]开发了E/CRC模型，可以预测弯头、三通和其他一些管件的侵蚀。BISWAS等[15]基于冲击参数、表面材料特性和能量因素开发了一种可以准确预测试验冲蚀值的冲蚀模型。但现有模型都只是侧重于阐述冲蚀磨损的部分机理，并没有综合其他的冲蚀理论。笔者选用固体微小颗粒在弯管壁面的冲蚀速率（Rerosion）表征弯管的冲蚀程度，且涉及微小颗粒的质量流量、重力方向以及颗粒的大小对冲蚀的影响，根据综合影响因素，选用OKA等[16-17]的冲蚀模型最为合适。具体为：

式中：ρw为靶材的密度（g/cm3）；Hv为靶材的维氏硬度（HV）；dp为粒子直径，（μm）；d'为参考直径（μm）；V'为参考粒子的冲击速度（m/s），参数如表1所示。

1.3 颗粒碰撞模型

固体颗粒对管壁的撞击是一种非弹性碰撞，且存在动量损失，因此颗粒的反弹速度远不如其撞击速度。为了使颗粒的运动路径在数值模拟中更为精确，已有很多粒子壁面回弹模型[18-20]。笔者采用了一种经验弹性恢复计算公式：

式中：eN为法相弹性恢复系数；eT为切相弹性恢复系数；θ为入射角，（°）。

笔者采用分段线性方式设置冲击角函数与入射角参数的关系，如表2所示。