近年来,随着管道建设水平的提高,我国油气管道干线总长度已超过160 000 km[1],作为关系能源的“国脉”,管道的安全与环保成为社会各界关注的焦点。然而,管道在长期油气输送中易受腐蚀、第三方破坏、建造缺陷以及自然灾害等因素影响而产生缺陷,一旦管道的承压能力不足则容易引发泄漏、燃烧爆炸等事故,因此需要对含缺陷管道进行及时补强。而环焊缝作为管道输送系统的薄弱环节,是较易发生失效的部位,国内外对于高级别钢的环焊缝缺陷一般采用B型套筒的补强方式[2-3]。与换管修复方式相比,B型套筒可以在役施工,施工时仅需进行适当降压、限流操作,修复成本仅为换管成本的10%,从而广泛应用于管道环焊缝缺陷修复之中。
大量研究表明,B型套筒在焊接过程中,套筒纵向对接焊缝对管道本体不会产生影响,但是连接管道和套筒的环向搭接角焊缝会产生残余应力和较高的管壁温度[4],而可能使环向搭接角焊缝中生成裂纹,也可能使原管道中的环焊缝裂纹在补强后继续服役的过程中发生扩展[2,6],如果环焊缝最终完全开裂,B型套筒角焊缝能承受的极限弯矩则骤降为原管道母材的69.0%[5]。
但这些研究多集中于结构力学性能方面,针对B型套筒结构的无损检测,国内研究仍处于起步阶段,且多着眼于套筒搭接角焊缝缺陷的检测。黄磊等[7]利用仿真软件结合相控阵超声“三角区域分析法”对缺陷图谱进行评判,降低了B型套筒搭接焊缝缺陷评定的盲目性。刘琰等[8]通过数值模拟和试验,发现通过相控阵超声扇扫得到的缺陷回波信号峰值与孔型缺陷直径呈正相关,为孔型缺陷的定量分析提供了一种可靠的手段。为进一步分析相控阵超声检测方法对于B型套筒角焊缝内部缺陷的检测能力,张宏博等[9]建立了有限元模型并结合试验验证,分析和比较了不同相控阵超声检测方法对于焊缝内部缺陷的检测能力,发现采用横波相控阵较纵波相控阵对B型套筒角焊缝内部缺陷的检测,具有更好的聚焦效果,缺陷识别更精确。
这些研究为套筒搭接角焊缝的检测提供了比较完善的检测方案,但是由于B型套筒与原管道之间存在空气层,难以采用常规无损检测方式(如超声、射线检测等)进行原管道环焊缝中缺陷的检测,而管道爬行器等检测装置又难以进行在役检测,故原管道环焊缝检测是套筒无损检测领域的一个难点。考虑到导波可以在板类结构或管状结构中传播很长一段距离,而且在薄板和长距离管线检测中已有一定的应用,为此文章尝试采用导波对原管道环焊缝中的裂纹扩展深度进行定量检测。
1. 检测系统的硬件架构与检测方案
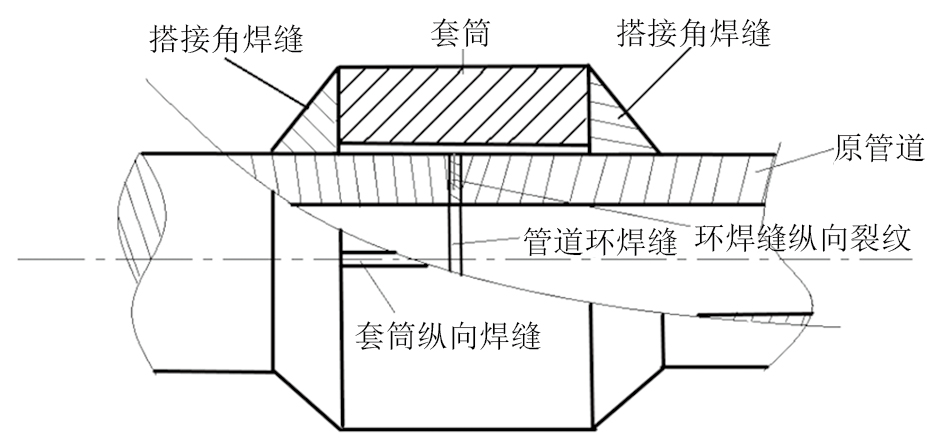
B型套筒补强结构示意如图1所示,B型套筒一般为两个半圆筒通过焊接安装而成,套筒两端通过角焊缝与待修复管道连接,通过搭接角焊缝,套筒与原结构紧密结合并将损坏的环焊缝封在套筒内部。大量试验及工程应用数据显示,被评价为必须进行修复的高危管道,相较于更换管段,采用B型套筒补强技术修复成本降低60%~85%[4],并且修复后管道的安全性与换管相当。
基于试验室已有条件,文章试验构建的检测系统如图2所示,采用纵向振动的PWAS(压电晶片主动传感器)阵列同时或者分组激励以在管道整个截面或者周向局部产生轴向导波;采用函数发生器产生汉宁窗包络,其包含5个周期的时域短脉冲,可对压电片进行窄带激励,以在特定的中心频率上激励特定的导波;采用示波器整体提取或者分组提取套管结构另一侧的导波信号并存储,将其与仿真数据库进行互相关分析,反演得到压电阵列轴向覆盖区域中环焊缝裂纹深度与横向尺寸信息。
具体检测流程如图3所示,其中关键的研究内容包括导波模式与频率选择,收发压电阵列设计;主要设计要求包括使主要声能经由原管道通过套筒补强结构以及增加接收信号幅值与原管道环焊缝中裂纹深度的相关性;主要试验测量包括材料参数(如声速、尺寸)测量以及信号测量等内容。其中关于优选导波模态与频率的研究涉及搭接角焊缝处的导波散射问题,前期已经采用模式展开法以及有限元仿真模型进行了设计与验证。研究表明100 kHz A0模态从外部入射补强结构时约有80%的能量通量经过角焊缝进入原管道;相同情况下53 kHz S0模式约有70%的能量通量通过角焊缝进入原管道[10]。考虑到管道径厚比较大,且现有研究只考虑轴向导波,因此采用兰姆波标记方法。以下主要围绕压电阵列的设计来介绍方案的具体设计过程。
2. 导波模态、频率选择与PWAS长度的设计
PWAS基于压电效应工作,耦合了力(机械)和电(应变Sij、机械应力Tkl、电场Ek、电位移Dj)的效应,一维压电应力本构方程如下
| {�1=�11��1+�31�3�3=�31�1+�33��3 | (1) |
式中:S1为应变;T1为机械应力;D3为电位移;E3为电场;�11�为无外加电场时材料的柔度系数;�33�为PWAS不受应力作用时的介电常数;d31为压电常数,代表力电耦合效应。
PWAS和结构之间通过黏合剂层实现激励和接收超声波。在理想黏贴情况下,胶层的剪应力集中于PWAS的两端(故此模型被称为钉扎力模型),取其大小为τa,若PWAS的长度为2a,则切应力力源函数可以表示为[11]
| �(�)=���[�(�+�)-�(�-�)] | (2) |
式中:x为PWAS的长度坐标;δ为狄拉克函数。
因此在波导中产生的兰姆波应变与位移可以表示为波数的导波模式叠加;其中每个模式的幅值同时由波数ξj的函数A(ξj)和以ξja为因变量的调制函数决定。A(ξj)由留数定理结合频散方程确定,具体形式见文献[11],和晶片长度a无关,此处不再赘述;由调制函数可知,当PWAS的长度是λj/2的奇数倍时最大,偶数倍时最小。由于兰姆波幅值随频率发生改变,考虑到在频厚积比较大,兰姆波模式较多时,各模式的调制函数最大值和最小值的变化复杂,要激励单一模式则相对困难[12],故文章在两个优选频率与模式的组合中选择激励低频的53 kHz S0模式,而不是超过A1截止频率,100 kHz的A0模式。
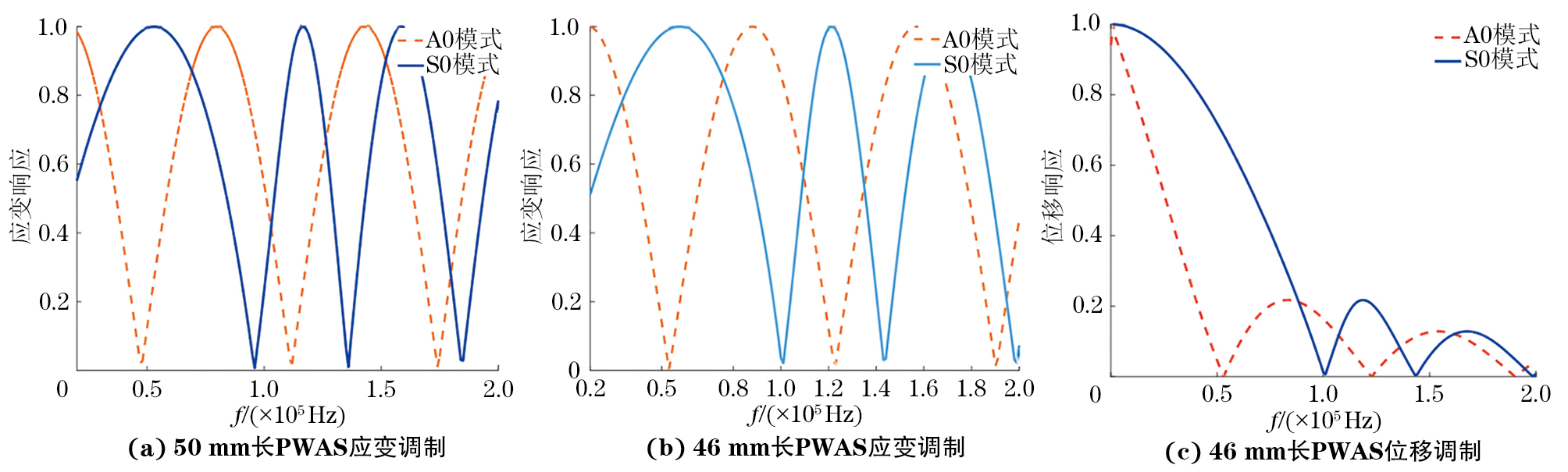
图4(a)为PWAS的长度等于53 kHz S0模式的半波长(50 mm)时,A0模式和S0模式的sin|ξa|随频率的变化关系。可以看到此时虽然S0模式的应变调制达到了峰值,但其也有着不小的应变调制。若将PWAS的长度调整为46 mm时,如图4(b),(c)所示,在53 kHz,A0模式受到抑制,而S0模式有不小的应变和位移调制幅度。因此优选46 mm长的PWAS在53 kHz频率下激励出单一的S0模态。
3. 有限元仿真与信号数据库的建立
作为检测方案可行性验证的第一步,文章以下的仿真与试验中均设定环焊缝中纵向裂纹贯穿整个周长。
为了减少计算工作量,采用轴对称二维有限元模型进行管道导波检测仿真。在轴对称模型中,代表母管的矩形角坐标设置的r和z为(87 mm,0 mm)。被检测结构的轴对称有限元建模示意如图5所示,根据测量,设定管道外径为109.5 mm,厚度为22.5 mm,长度为3 000 mm;套筒厚度和长度分别为30 mm和100 mm;套筒与母管间隙为2.5 mm。模型中所使用的PWAS长度为46 mm,厚度可变。
构建几何模型和设置材料属性之后,对模型设置边界条件,由于需要得到时域信号,所以采用“瞬态”进行研究。对PWAS设置为“压电材料”,对套筒模型设置为“线弹性材料”,其材料参数如表1,2所示。采用“电路”模块对PWAS进行设置,通过“电压源”和“外部终端”设置所需的激励信号为
| ����=1-cos(2��0�/�) | (3) |
式中:f0=53 kHz,为激励的中心频率,其目的是为给正弦信号加窗;t为时间;取n=3以限制信号的时域宽度。
| 材料 | 密度ρ/(kg · m-3) |
杨氏模量 /Pa |
纵波衰减/(dB · m-1) | 横波衰减/(dB · m-1) | 泊松比 |
|---|---|---|---|---|---|
| 钢 | 7 850 | 2.034×109 | 130.826 7 | 88.991 1 | 0.290 |